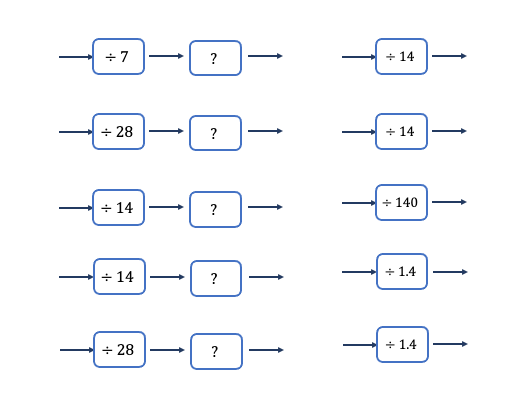
Consider the following set of three questions.
How would your pupils cope with this idea in this context? What if it was in the context of related calculation, dividing decimals, dividing numbers in standard form, algebraic division, fraction multiplication and division, or proportion?
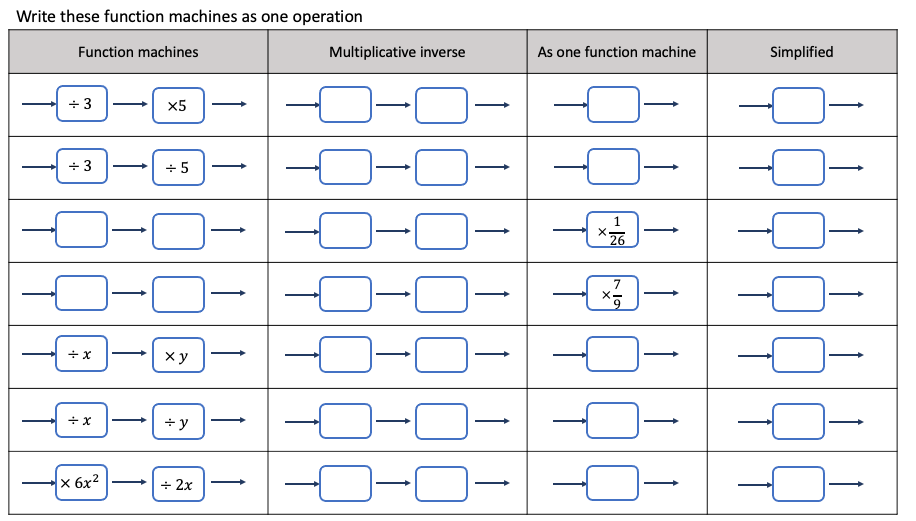
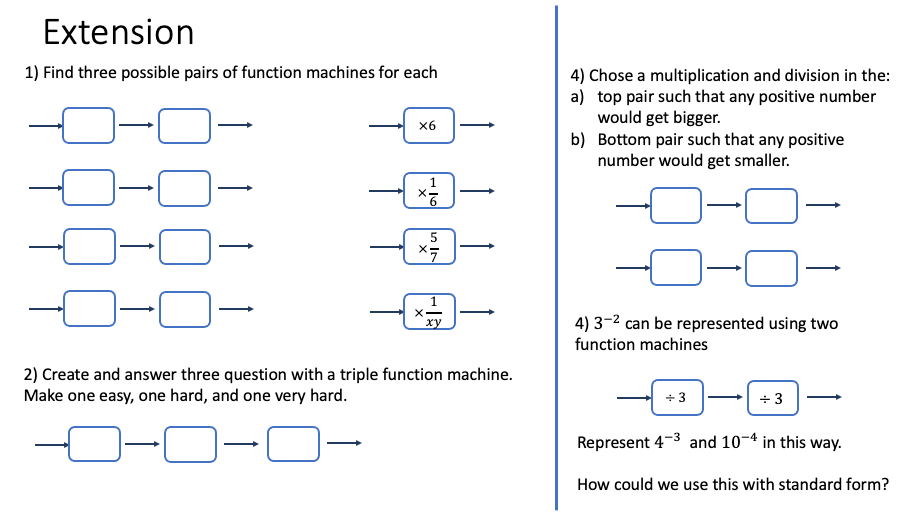
In this task, I attempt to deepen students understanding of the properties of division, and the associativity of division for example 120 ÷ 6 ÷ 3 is the same as 120 ÷ (6 x 3), 120 ÷ 6 x 3 is the same as 120 ÷ (6 ÷ 3).
I am trying to build on the bigger idea of using the multiplicative inverse instead of division, e.g. multiply by a third instead of dividing by three. Multiplication behaves, division less so, this is why I believe that viewing division in this way could perhaps help pupils be more flexible with calculations and it could transfer to other areas of maths better. As a stand-alone task, this may not be worthwhile, and may not help pupils understand these ideas, but by regularly incorporating these into the curriculum, it may help pupils build connections between different areas of maths. One of the ways that I am the most excited about is to avoid the need for pupils to unitize when working with proportion, for example, seeing that ÷ 11 x 6 is the same as multiplying by 6 elevenths.
Please note that there would need to be a lot of groundwork done prior to this task on the multiplicative inverse, multiplying fractions, pictorial or concrete representations (example below courtesy of @mrshawthorne7) along with analogies of division e.g stories of repeated sharing.
What are your thoughts on thinking about division in this way, where could it help students in the future, what might the barriers or disadvantages be?
Comments