I showed one of these types of problems to my class.
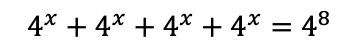
They struggled and weren't sure how to proceed with the problem. I highlighted how addition could be represented as multiplication, did some basic example, and then built them up to this problem, job done? About two months later in a delayed topic test, I think a similar question was the worst answered question on the paper, and so I have designed this task to give students more practice with this idea.
It requires an understanding of other index properties such as changing base, solving equations involving indices, and negative and fractional powers. This task may be a little procedural and you may want to cut down on the number of questions, but I believe that the number of other skills used will keep pupils having to think through the entirety of the task.
Hopefully, this task is of some use to you. I would love any feedback, both positive and constructive.
Love the task, and here is my feedback/suggestions (feel free to ignore, especially if it doesn't work for your class context):
In Q1 I would love to see the last few questions rapidly increasing in demand (somewhat akin to Increasingly Difficult Questions). So I would be tempted to put in some where the base is a negative, fractions, decimals, algebraic expressions (especially with more than one term) - but then may need to change the questions instructions from 'Simplify' to 'Write as a single power' (or something to that effect)
Although this is now diverging from your main task/purpose... but perhaps have the same magnitude for the bases but the negatives having an even index... eg (-2)^5 + 2^5