I like to look at sequences additively, for example, the sequence 3n+2 is the sequence 3n; 3, 6, 9, 12... plus the constant sequence 2: 2, 2, 2, 2.
I believe this approaches scales well to quadratic sequences, these can be thought of as a pure quadratic sequence plus a linear sequence. This is why subtracting the pure quadratic sequence and then find the nth term of the remainder is my personal approach for finding the nth term for quadratic equations.
To help develop a conceptual understanding of this approach, I believe it is important that pupils see generating and finding the nth term be opposites of each. Therefore, I have created this task to highlight the additive nature of sequences when generating them.
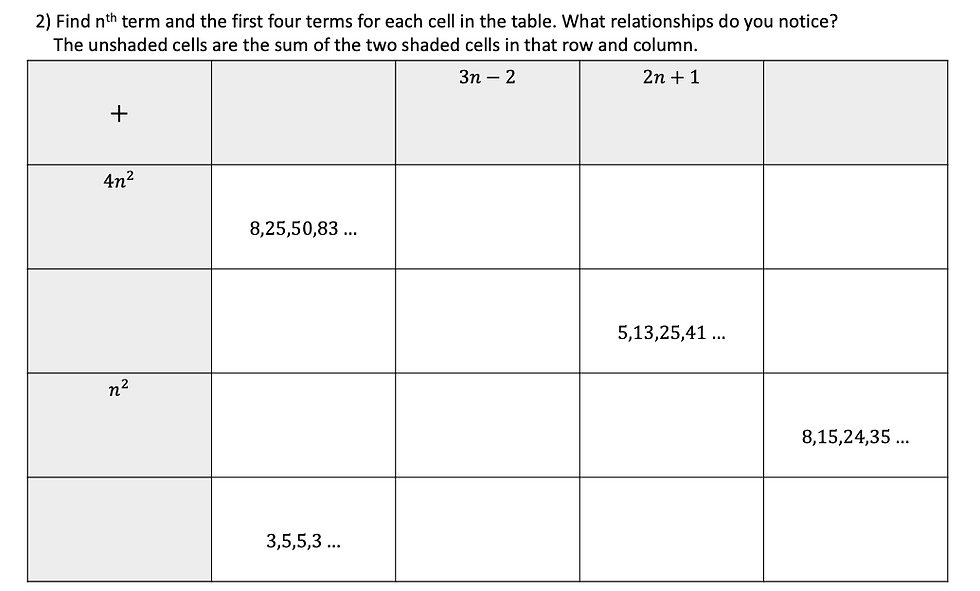
Once pupils have a basic understanding of quadratic sequences, I would ask them to make the following sequences.
Pupils would then use these sequences to try and complete the grids. Notice that for the last row and the last column pupils must work backward, subtracting sequences, and the idea is extended further in question 2. This is laying the groundwork for finding the nth term of a quadratic sequence. (Note I have given the sequence 13, 31, 59, 97 even though it is unnecessary to act as a check for pupils.)
There are a lot of patterns to be noticed competing the grid, draw pupils' attention to how the sequences change as you move down, or move across.
Question 3 deviates from the main purpose of the task, the additive nature, and shows how quadratic sequences can also be thought of as the product of two linear sequences. I find the (n+1)(n+1) box particularly lovely!
(Note: Pupils must be able to factories non-monic quadratics)
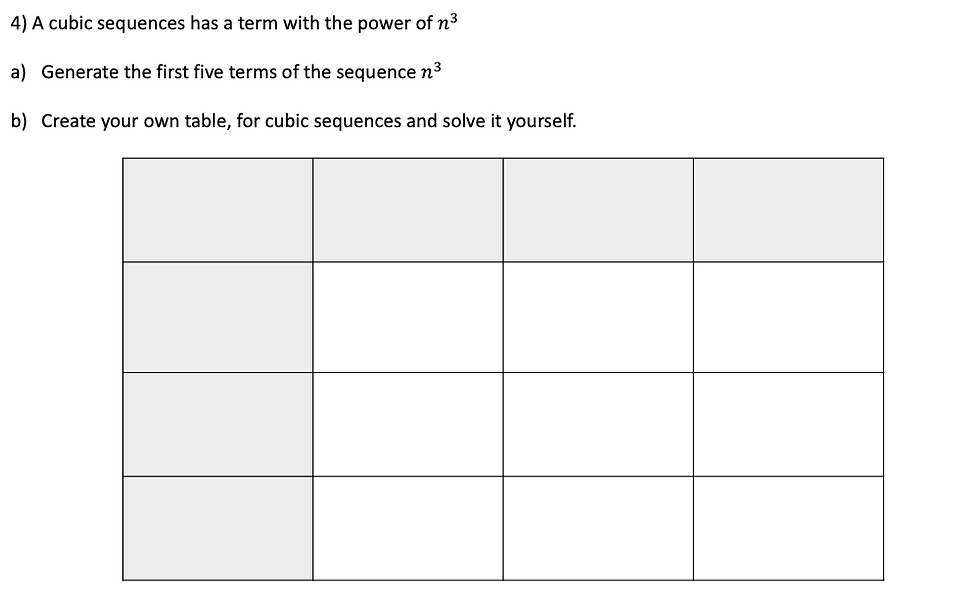
Question 4 is extension work, getting pupils to apply the principles from the task so far and use them for cubic sequences. It gives them the opportunity to be creative and explore.
Comments