Bar Modelling for the mean

I have previously used Don Stewards great towers resource, and this is a brilliant representation to understand the mean. I would then move from this to the abstract. However, I have now added a step, bar modeling. I found it to be particularly powerful, and feel it highlights the continuousness of number. It can also be extended for more complex problems as I shall discuss below.

There is a great applet on Boss Maths, pictured below, which I highly recommend. I have used this model as a basis for my representations.

I would like you to try and model the following problems before having a look at my models.

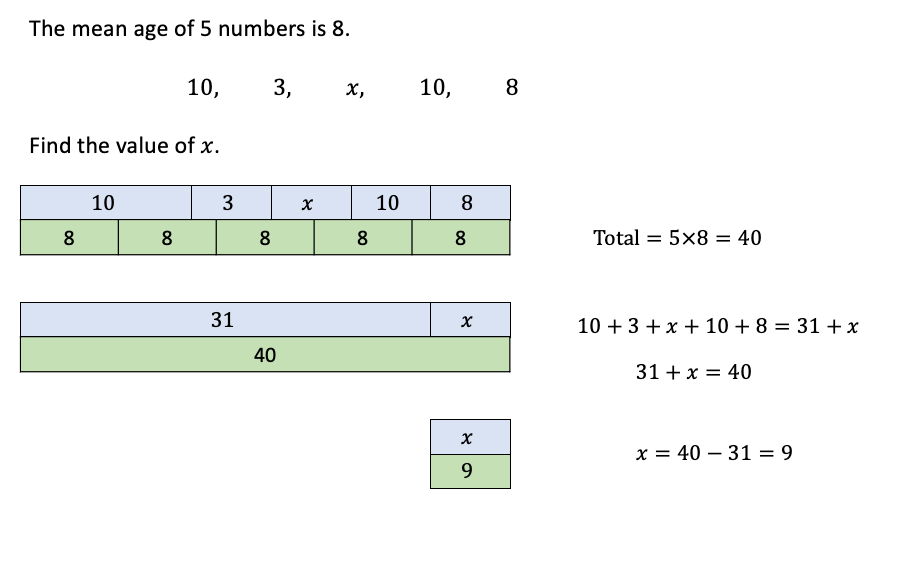
a) The mean of 5 numbers is 8. The numbers are 10, 3, x, 10, 8.

Find the value of x.

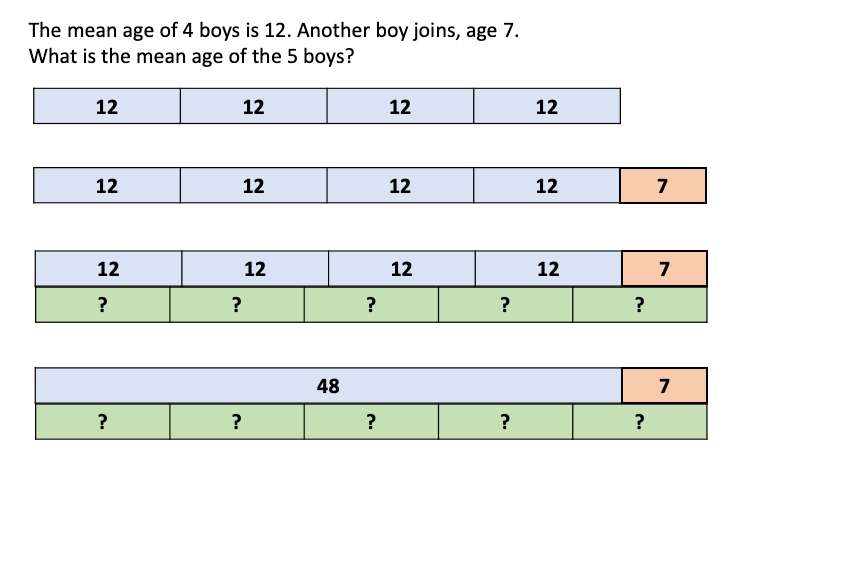
b) The mean age of 4 boys is 12. Another boy joins, age 7.

What is the mean age of the 5 boys?

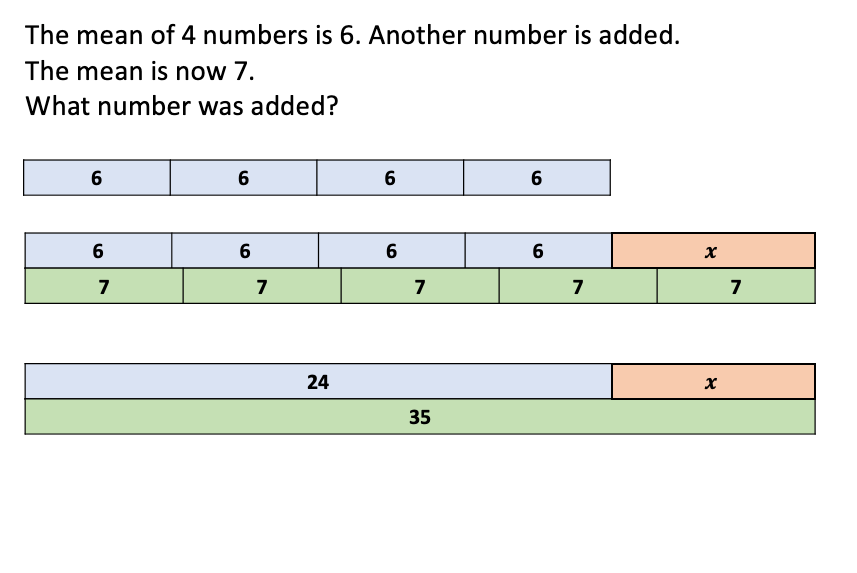
c) The mean of 4 numbers is 6. Another number is added.

The mean is now 7. What number was added?

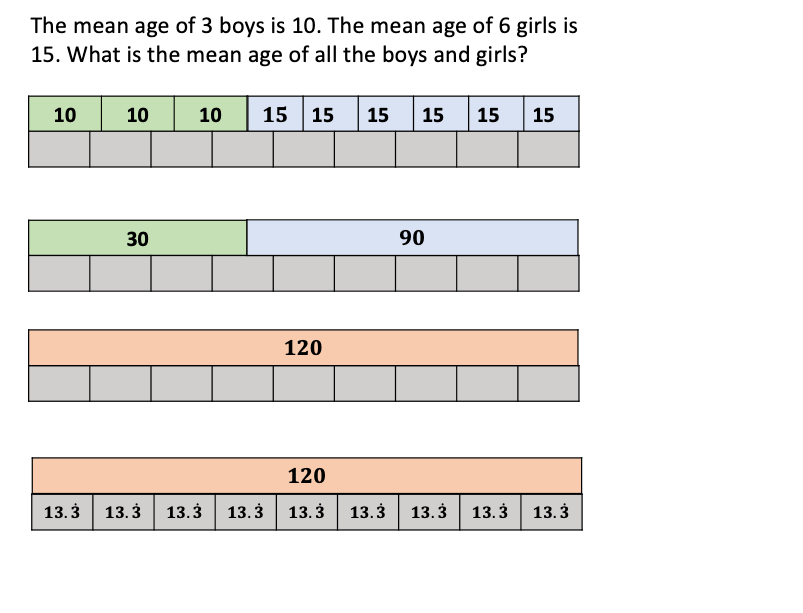
d) The mean age of 3 boys is 10. The mean age of 6 girls is 15.

What is the mean age of all the boys and girls?

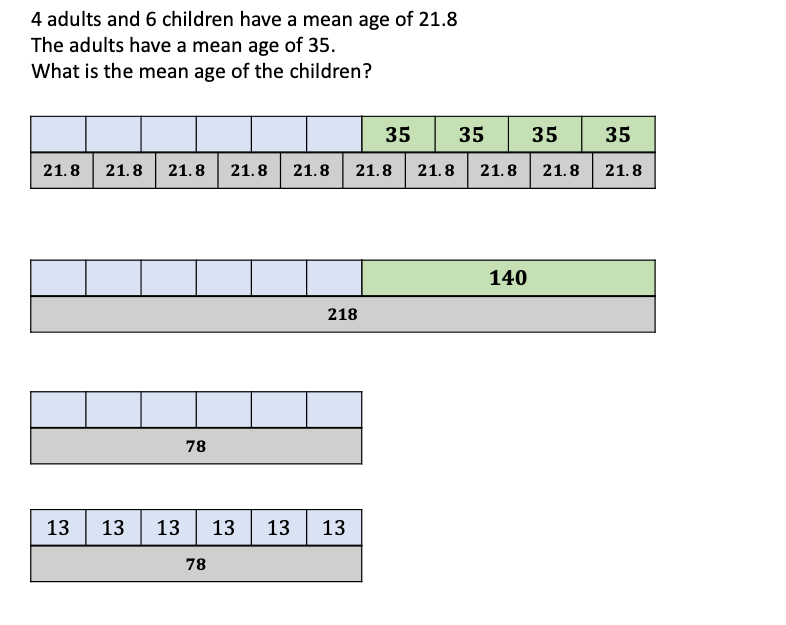
e) 4 adults and 6 children have a mean age of 21.8

The adults have a mean age of 35. What is the mean age of the children?

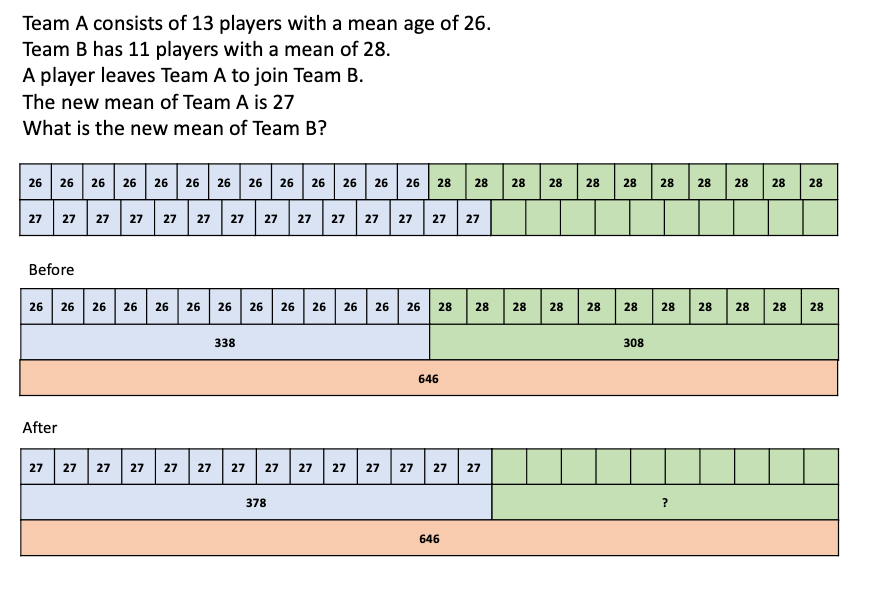
f) Team A consists of 13 players with a mean age of 26. Team B has 11 players with a mean of 28. A player leaves Team A to join Team B.

The new mean of Team A is 27. What is the new mean of Team B?

The last one is probably a bit impractical to do by hand and highlights the need for an extra strategy. I would recommend using written methods alongside and using the models and a way to understand the process. Pupils could create their own models for a few problems, compare them, or even match them to written methods.

Haven got in touch with Sudeep he has now updated his applet to include these representations, for which I am incredibly grateful, his site is brilliant, please check it out.

I have personally have found these to be really successful, hopefully, they are of some use to you too. Any feedback is much appreciated.

Download here